初二（上）首次月考数学试题
1、选择题（每题2分）
1．（2分）下列各式中，肯定是二次根式的有（）
①
②
③
④
⑤
A．2个 B．3个 C．4个 D．5个
2．（2分）若等式
成立，则m的取值范围是（）
A．m≥﹣2 B．m≥2 C．﹣2≤m≤2 D．m≥4
3．（2分）下列说法中，正确的是（）
A．被开方数不一样的二次根式肯定不是相同种类二次根式
B．只有被开方数一模一样的二次根式才是相同种类二次根式
C．相同种类二次根式肯定都是最简二次根式
D．两个最简二次根式可能不是相同种类二次根式
4．（2分）下列关于x的二次三项式在实数范围内不可以够因式分解的是（）
A．x2﹣3x+2 B．x2﹣
x+1 C．2x2﹣xy﹣y2 D．x2+3xy+y2
5．（2分）在一元二次方程ax2﹣3x+c＝0（a≠0）中，若a、c异号，则方程（）
A．根的状况没办法确定 B．没实数根
C．有两个不相等的实数根 D．有两个相等的实数根
6．（2分）如图所示，在一幅长80cm，宽50cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图．假如要使整幅挂图的面积是5400cm2，设金色纸边的宽为xcm，那样x满足的方程是（）
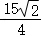
A．x2+130x﹣1400＝0 B．x2+65x﹣350＝0
C．x2﹣130x﹣1400＝0 D．x2﹣65x﹣350＝0
2、填空题（每题2分）
7．（2分）假如代数式
有意义，那样x的取值范围是__________．
8．（2分）已知xy＜0，则
＝__________．
9．（2分）若
与
是相同种类二次根式，那样整数x可以是__________（写出一个即可）．
10．（2分）
﹣2的倒数是__________．
11．（2分）计算：（
﹣1）2016•（﹣﹣1）2017＝__________．
12．（2分）概念一种新运算：a*b＝
•
﹣
，则3*4＝__________．
13．（2分）一元二次方程（x+1）（1﹣x）＝2x化成二项系数为正的一般式是__________．
14．（2分）方程x（x+1）＝2的根为__________．
15．（2分）假如关于x的方程mx2+2（m+1）x+m＝﹣1有两个实数根，那样m的取值范围是__________．
16．（2分）已知（x2+y2）2﹣y2＝x2+6，则x2+y2的值是__________．
17．（2分）一个两位数，它的数值等于它的个位上的数字的平方的3倍，它的十位数字比个位数字大2．若设个位数字为x，列出求该两位数的方程式为__________．
18．（2分）某厂计划在两年内把产量提升44%，假如每年比上一年的增长率相同，那样增长率为__________．
3、简答卷（每题5分）
19．（5分）计算：
﹣
+﹣3
．
20．（5分）计算：
÷
．
21．（5分）（﹣
）÷
．
22．（5分）计算：
23．（5分）解方程：4（2x﹣1）2﹣36＝0．
24．（5分）2（x﹣3）2＝x（x﹣3）
25．（5分）解方程：（2x+1）2+3（2x+1）+2＝0．
26．（5分）解方程：
﹣3x﹣5＝0．
27．（5分）在实数范围内因式分解：2x2﹣3xy﹣3y2．
28．（5分）在实数范围内因式分解：﹣2a2b2+ab+2．
4、解答卷（28题6分，29题8分）
29．（6分）某商场销售一批衬衣，平均天天可售出20件，每件盈利40元，为了扩大销售，增加收益，尽可能降低库存，商场决定采取适合的降价手段，经调查发现，假如每件衬衣降价1元，商场平均天天可多售出2件，若商场天天要获收益1200元，请计算出每件衬衣应降价多少元？
30．（8分）已知：关于x的方程x2﹣（k+2）x+2k＝0．
（1）求证：无论取任何实数值，方程总有实数根；
（2）若等腰三角形ABC的一边长a＝1，另两边长b＝c，恰好是这个方程的两个根，求△ABC的周长．
参考答案与考试试题分析
1、选择题（每题2分）
1．（2分）下列各式中，肯定是二次根式的有（）
①②③④⑤
A．2个 B．3个 C．4个 D．5个
【剖析】借助二次根式概念判断即可．
【解答】解：①是二次根式；
②，当a≥0时是二次根式；
③是二次根式；
④是二次根式；
⑤，当x≤0时是二次根式，
故选：B．
2．（2分）若等式成立，则m的取值范围是（）
A．m≥﹣2 B．m≥2 C．﹣2≤m≤2 D．m≥4
【剖析】直接借助二次根式有意义的条件剖析得出答案．
【解答】解：∵等式
成立，
∴
，
解得：m≥2．
故选：B．
3．（2分）下列说法中，正确的是（）
A．被开方数不一样的二次根式肯定不是相同种类二次根式
B．只有被开方数一模一样的二次根式才是相同种类二次根式
C．相同种类二次根式肯定都是最简二次根式
D．两个最简二次根式可能不是相同种类二次根式
【剖析】依据相同种类二次根式的定义判断．
【解答】解：A、被开方数不一样的二次根式可以是相同种类二次根式，本选项说法错误；
B、化简后被开方数一模一样的二次根式才是相同种类二次根式，本选项说法错误；
C、相同种类二次根式未必都是最简二次根式，本选项说法错误；
D、两个最简二次根式可能不是相同种类二次根式，本选项说法正确；
故选：D．
4．（2分）下列关于x的二次三项式在实数范围内不可以够因式分解的是（）
A．x2﹣3x+2 B．x2﹣x+1 C．2x2﹣xy﹣y2 D．x2+3xy+y2
【剖析】将各选项整式分别分解即可判断．
【解答】解：A、x2﹣3x+2＝（x﹣1）（x﹣2），不符合题意；
B、x2﹣x+1在实数范围内不可以因式分解，符合题意；
C、2x2﹣xy﹣y2＝（x﹣y）（2x+y），不符合题意；
D、x2+3xy+y2＝（x+y）（x+
y），不符合题意；
故选：B．
5．（2分）在一元二次方程ax2﹣3x+c＝0（a≠0）中，若a、c异号，则方程（）
A．根的状况没办法确定 B．没实数根
C．有两个不相等的实数根 D．有两个相等的实数根
【剖析】由a、c异号可得出9﹣4ac＞0，即△＞0，进而可得出一元二次方程ax2﹣3x+c＝0（a≠0）有两个不相等的实数根．
【解答】解：△＝（﹣3）2﹣4ac＝9﹣4ac．
∵a、c异号，
∴﹣ac＞0，
∴9﹣4ac＞0，即△＞0．
∴一元二次方程ax2﹣3x+c＝0（a≠0）有两个不相等的实数根．
故选：C．
6．（2分）如图所示，在一幅长80cm，宽50cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图．假如要使整幅挂图的面积是5400cm2，设金色纸边的宽为xcm，那样x满足的方程是（）
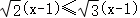
A．x2+130x﹣1400＝0 B．x2+65x﹣350＝0
C．x2﹣130x﹣1400＝0 D．x2﹣65x﹣350＝0
【剖析】依据矩形的面积＝长×宽，得出本题的等量关系是：（风景画的长+2个纸边的宽度）×（风景画的宽+2个纸边的宽度）＝整个挂图的面积，由此可得出方程．
【解答】解：依题意，设金色纸边的宽为xcm，
（80+2x）（50+2x）＝5400，
整理，得x2+65x﹣350＝0．
故选：B．
2、填空题（每题2分）
7．（2分）假如代数式
有意义，那样x的取值范围是__________________________________________________．
【剖析】依据被开方数大于等于0，分母不等于0列式计算即可得解．
【解答】解：由题意得，x+2≥0且x﹣1≠0，
解得x≥﹣2且x≠1．
故答案为：x≥﹣2且x≠1．
8．（2分）已知xy＜0，则
＝____________________
__________．
【剖析】依据二次根式的运算法则即可求出答案．
【解答】解：xy2＝x•xy，xy＜0，
∴x＞0，y＜0
原式＝|y|
＝﹣y
故答案为：﹣y
9．（2分）若与是相同种类二次根式，那样整数x可以是__________（写出一个即可）．
【剖析】依据相同种类二次根式的定义列式计算即可．
【解答】解：＝2，
由题意得，x+2＝5，
解得，x＝3，
故答案为：3（答案不唯一）．
10．（2分）
﹣2的倒数是__________
__________．
【剖析】依据分母有理化进行计算即可得到结论．
【解答】解：﹣2的倒数是＝
＝，
故答案为：．
11．（2分）计算：（
﹣1）2016•（﹣
﹣1）2017＝____________________．
【剖析】先借助积的乘方得到原式＝﹣[（﹣1）（+1）]2016•（+1），然后借助平方差公式计算．
【解答】解：原式＝﹣[（﹣1）（+1）]2016•（+1）
＝﹣（2﹣1）2016•（+1）
＝﹣﹣1．
12．（2分）概念一种新运算：a*b＝
•﹣，则3*4＝__________
__________．
【剖析】依据*的运算办法，用4和3的积的算术平方根减去它们的商的算术平方根，求出算术的值是多少即可．
【解答】解：∵a*b＝
•
﹣
，
∴3*4
＝
•
﹣
＝2﹣
＝
故答案为：．
13．（2分）一元二次方程（x+1）（1﹣x）＝2x化成二项系数为正的一般式是____________________________________________________________．
【剖析】直接借助多项式乘以多项式，进而得到一元二次方程一般形式．
【解答】解：（x+1）（1﹣x）＝2x
1﹣x2＝2x，
则﹣x2﹣2x+1＝0，
故x2+2x﹣1＝0．
故答案为：x2+2x﹣1＝0．
14．（2分）方程x（x+1）＝2的根为__________．
【剖析】第一将原方程整理为一般式，然后再分解因式求解．
【解答】解：原方程可化为：x2+x﹣2＝0，
（x﹣1）（x+2）＝0，
解得x1＝1，x2＝﹣2．
15．（2分）假如关于x的方程mx2+2（m+1）x+m＝﹣1有两个实数根，那样m的取值范围是__________________________________________________．
【剖析】由二次项系数非零及根的辨别式△≥0，即可得出关于m的一元一次不等式组，解之即可得出m的取值范围．
【解答】解：原方程可变形为mx2+2（m+1）x+m+1＝0．
∵该方程有两个实数根，
∴，
∴m≥﹣1且m≠0．
故答案为：m≥﹣1且m≠0．
16．（2分）已知（x2+y2）2﹣y2＝x2+6，则x2+y2的值是__________．
【剖析】设x2+y2＝z，原式变为关于z的一元二次方程，因式分解法求得z的值，即可求得x2+y2＝3．
【解答】解：设x2+y2＝z，则原式变为z2﹣z﹣6＝0，
（z﹣3）（z+2）＝0，
解得z1＝3，z2＝﹣2，
∵设x2+y2≥0，
∴设x2+y2＝3，
故答案为3，．
17．（2分）一个两位数，它的数值等于它的个位上的数字的平方的3倍，它的十位数字比个位数字大2．若设个位数字为x，列出求该两位数的方程式为________________________________________________________________________________．
【剖析】设个位数字为x，则这个数为3x2，十位数字为x+2，依据题意表示出这个两位数，列出方程．
【解答】解：设个位数字为x，则这个数为3x2，十位数字为x+2，
由题意得，10（x+2）+x＝3x2．
故答案为：
10（x+2）+x＝3x2．
18．（2分）某厂计划在两年内把产量提升44%，假如每年比上一年的增长率相同，那样增长率为__________．
【剖析】设增长率为x，依据两年内把产量提升44%，即可得出关于x的一元二次方程，解之取其正值即可得出结论．
【解答】解：设增长率为x，
依题意，得：（1+x）2＝1+44%，
解得：x1＝0.2＝20%，x2＝﹣2.2（不合题意，舍去）．
故答案为：20%．
3、简答卷（每题5分）
19．（5分）计算：﹣
+﹣3
．
【剖析】先化简各二次根式，再合并相同种类二次根式即可得．
【解答】解：原式＝4﹣+﹣
＝．
20．（5分）计算：
÷．
【剖析】依据二次根式的乘法法则进行计算即可．
【解答】解：÷
＝（1÷
×4）
＝（1×
）
＝10．
21．（5分）（
﹣）÷．
【剖析】先通分，再分母有理化，计算即可．
【解答】解：原式＝
×
＝
×
＝
＝
＝a．
22．（5分）计算：
【剖析】直接借助一元一次不等式的解法将原式变形进而计算即可．
【解答】解：
x﹣≤
x﹣，
故（﹣）x≤﹣，
解得：x≥1．
23．（5分）解方程：4（2x﹣1）2﹣36＝0．
【剖析】依据直接开办法即可求出答案．
【解答】解：∵4（2x﹣1）2﹣36＝0，
∴（2x﹣1）2＝9，
∴2x﹣1＝±3，
∴x＝2或﹣1
24．（5分）2（x﹣3）2＝x（x﹣3）
【剖析】移项后分解因式，即可得出两个一元一次方程，求出方程的解即可．
【解答】解：移项得：2（x﹣3）2﹣x（x﹣3）＝0，
（x﹣3）[2（x﹣3）﹣x]＝0，
x﹣3＝0，2（x﹣3）﹣x＝0，
x1＝3，x2＝6．
25．（5分）解方程：（2x+1）2+3（2x+1）+2＝0．
【剖析】设2x+1＝y，则原方程可化为：y2+3y+2＝0，解之求得y之后，即可得．
【解答】解：设2x+1＝y，则原方程可化为：y2+3y+2＝0，
∴（y+1）（y+2）＝0，
解得：y＝﹣1或y＝﹣2，
即2x+1＝﹣1或2x+1＝﹣2，
解得x1＝﹣1，x2＝﹣．
26．（5分）解方程：
﹣3x﹣5＝0．
【剖析】依据配办法即可求出答案．
【解答】解：∵﹣3x﹣5＝0，
∴x2﹣6x＝10，
∴x2﹣6x+9＝19，
∴（x﹣3）2＝19，
∴x＝3±
27．（5分）在实数范围内因式分解：2x2﹣3xy﹣3y2．
【剖析】解2x2﹣3xy﹣3y2＝0可得，x＝，依据求根公式的分解办法和特征可知：2x2﹣3xy﹣3y2＝2（x﹣）（x﹣
）．
【解答】解：当2x2﹣3xy﹣3y2＝0时，x＝，
所以2x2﹣3xy﹣3y2＝2（x﹣）（x﹣）．
28．（5分）在实数范围内因式分解：﹣2a2b2+ab+2．
【剖析】借助求根根式求得﹣2a2b2+ab+2＝0时a＝，则﹣2a2b2+ab+2＝﹣2（a﹣）（a﹣）．
【解答】解：令﹣2a2b2+ab+2＝0，则a＝，
所以﹣2a2b2+ab+2＝﹣2（a﹣）（a﹣）．
4、解答卷（28题6分，29题8分）
29．（6分）某商场销售一批衬衣，平均天天可售出20件，每件盈利40元，为了扩大销售，增加收益，尽可能降低库存，商场决定采取适合的降价手段，经调查发现，假如每件衬衣降价1元，商场平均天天可多售出2件，若商场天天要获收益1200元，请计算出每件衬衣应降价多少元？
【剖析】设每件衬衣应降价x元，依据均天天可售出20件，每件盈利40元，为了扩大销售，增加收益，尽可能降低库存，要降价，假如每件衬衣降价1元，商场平均天天可多售出2件，若商场天天要获收益1200元，可列方程求解．
【解答】解：设每件衬衣应降价x元，据题意得：
（40﹣x）（20+2x）＝1200，
解得x＝10或x＝20．
因题意要尽快降低库存，所以x取20．
答：每件衬衣至少应降价20元．
30．（8分）已知：关于x的方程x2﹣（k+2）x+2k＝0．
（1）求证：无论取任何实数值，方程总有实数根；
（2）若等腰三角形ABC的一边长a＝1，另两边长b＝c，恰好是这个方程的两个根，求△ABC的周长．
【剖析】（1）依据方程的各项系数结合根的辨别式得出△＝（k﹣2）2≥0，此题得证．
（2）当△＝0时，求出k值，进而找出方程的根，从而得出三角形的周长．
【解答】（1）证明：∵在方程x2﹣（k+2）x+2k＝0中，
△＝[﹣（k+2）]2﹣4×1×2k＝k2﹣4k+4＝（k﹣2）2≥0，
∴无论k取何值，方程总有两个实数根．
（2）解：当△＝（k﹣2）2＝0，即k＝2时，原方程为x2﹣4x+4＝0，
解得：x1＝x2＝2，
所以△ABC的周长为1+2+2＝5．
